Notion de cycle de phases
Les cycles de phases ou programme de phases permettent de :
-Sélectionner les signaux désirés en rejetant ceux qui ne contiennent pas d'information et qui, éventuellement, sont susceptibles de masquer d'autres signaux utiles.
-Discriminer le signe des fréquences en dimension f1.
-Compenser les imperfections d'une ou plusieurs impulsions de la séquence.
-Assurer une détection en quadrature optimale dans la dimension f2[1].
Chaque impulsion d'une séquence possède son propre cycle de phases qui peut-être plus ou moins complexe.
Le nombre d'accumulations idéal doit cependant être égal à un multiple du nombre de phases du cycle le plus long. Pour mieux comprendre cette méthode, une nomenclature standard a été définie (Fig7).
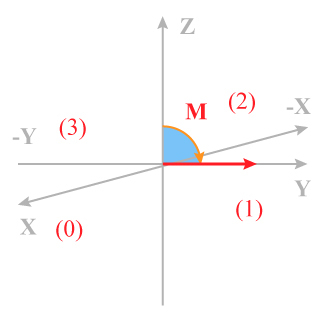
Exemple :
Exemple : Le cycle cyclops
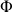= x, y, -x, -y, ou 0, 1, 2, 3.
Ce cycle impose l'accumulation d'un nombre multiple de 4 transitoires de précession libre.
La première impulsion
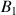se fait autour de x et la réception se fera en y, la deuxième impulsion se fera autour de -x et la réception en -x et la réception en -y, etc...
Il existe d'autres variantes de ce cycle comme ceux-ci dessous :
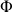= x, y, -x, -y, ou 0, 2, 1, 3.
Ou encore
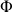= x, x, -x, -x, y, y, -y, -y ou 0, 0, 2, 2, 1, 1, 3, 3.
Ce dernier cycle impose un multiple de huit transitoires à accumuler.
