La spectroscopie de R.M.N à deux dimensions

La physique atomique nous enseigne que certains noyaux possèdent un moment cinétique de Spin P et également un moment magnétique 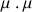est définie par la relation suivante 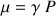avec 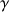qui est le rapport gyromagnétique, et 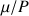est la constante caractéristique du noyau considéré.

En mécanique quantique, on décrit un système atomique au moyen de fonctions d'ondes, qui provient de la solution de l'équation de Schrödinger^[1].

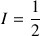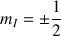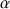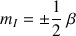Pour un proton, noyau à nombre quantique de spin où les fonctions d'ondes propres sont les suivantes : pour pour

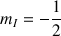
correspond au nombre quantique magnétique qui caractérise l'état stationnaire du noyau. Celui-ci est relié aux nombres de spins I du noyau. Le nombre total possible des états stationnaires ou propres du noyaux est donc égal à : 2I+1. Par conséquent le proton ne peut exister par rapport à son moment de spin que dans deux états stationnaires.

Hors champ magnétique les états 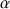et 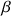ont la même énergie, on dit qu'ils sont dégénérés. Ce n'est que dans un champs magnétique statique homogène de valeur B₀ et par suite de l'interaction entre B₀ et 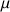que cette dégénérescence est levée (Fig.1). La séparation d'énergie ainsi produite qui est proportionnelle à l'intensité du champs B₀, crée la condition nécessaire à l'existence d'une transition spectroscopique et constitue ainsi la base de la spectroscopie par Résonance Magnétique Nucléaire.

Fig 1 : Énergie des états de spin en corrélation avec le champ BO [2].

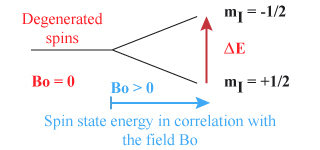
Le proton occupera l'état 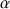(ou état de plus faible énergie) avec une probabilité plus grande.

Plus le champ B₀ augmente, plus la différence d'énergie (ou 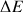) entre les deux états de spins augmente. On décrit la différence d'occupation de l'état fondamental et de l'état excité par la loi de Boltzmann.

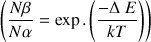
Avec 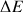qui est la différence d'énergie entre les deux états, k la constante de Boltzmann, T la température absolue en °K, 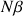le nombre de spins à l'état excité et 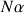 le nombre de spins à l'état fondamental.

Il n'existe à l'équilibre qu'un faible excès de noyau dans le niveau inférieur. Pour un champ de 1,4T à température ambiante 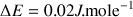. L'excès de population qui d'après la théorie est déterminant pour la probabilité d'une excitation ne dépasse pas 0.001%.