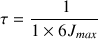The relayed COSY or one homonuclear step relayed COSY

A COSY spectrum may sometimes be inefficient to clearly identify all the signals, particularly if per chance two nuclei are equivalent. A typical example is that of peptides (Fig 19) where protons born by carbon of different amino acids have closed chemical shifts ; the COSY spectrum gives informations of the correlations between protons and protons in one hand and between 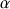protons and NH protons on the other hand.

Unfortunately, due to the overlapping of the 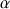protons signals, the attribution for the 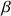protons signals can not be deduced from the NH protons (or the other way around). To solve this problem, we should be able to correlate the NH proton signals to those of the 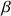protons; such a correlation may be obtained either by a long range COSY if the ⁴j coupling is not too weak or, better, by a relayed COSY experiment which allows the correlation of the signal from two nuclei at the only requirement that both of them are coupled to a third one^[1].

Fig. 19 : Schematic representation of the spectra COSY (left) and relayed COSY with two AMX type systems with Jax=0

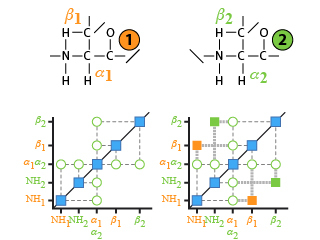
This experiment allows the differentiation of the belonging of the NH versus the 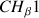or 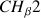. It is widely used for the sugar structure determination.

The pulse sequence of the experiment is derived from the COSY sequence in which the mixing pulse is followed by a fixed time and by a 90° pulse (Fig.20).

A 180° pulse, achieved in the middle of the new mixing period is also needed for the elimination of the evolution of the magnetization (refocalization) due to the chemical shifts during this additional delay.

Fig. 20 : The pulse sequence for the Relayed COSY

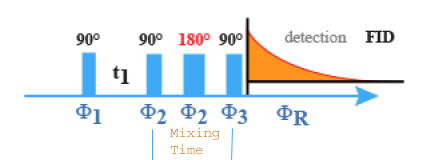
Applied to the AMX type system, this pulse sequence achieves a first coherence transfer from A to M as that one observed in the COSY experiment.

During the mixing time, the magnetizations evolve in such a wav that ideally the different components of the magnetization of the M nucleus are in antiphase versus the 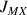coupling.

The third impulsion at 90° achieves then the transfer from the M nucleus toward the X nucleus.

The phase cycles of the impulsions and of the receiver is derived from that of the COSY experiment.

However, it needs an additional base cycle for the elimination of the artefacts due to transfers of the NOESY type. This consists to inverse the phase of the second impulsion without modifying the reception phase. The result is a global cycle with 8 components:

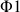=0, 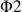=0 0 1 1 2 2 3 3, 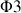=0 2 1 3, 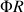= 0 0 2 2

For optimizing the mixing time, we have to define the delay between each impulsion. This one is deduced from the following formula where 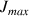stands for the value of the biggest coupling constant: