The spin ½ nuclei seen by the quantum mechanic
The example of the proton
The atomic physic teaches us that some nuclei have a kinetic momentum due to their spin state: P and also a magnetic momentum
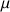, which is defined by the following relation:
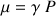where
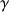is the gyro magnetic ratio, thus
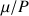characterizes a given nucleus.
The quantum mechanic describes an atom with wave functions solution of the Schrödinger[1] equation.
For a proton, nucleus with spin quantic number
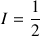, or
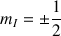the own wave functions are the following:
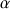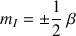for
for
.
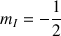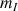corresponds to the magnetic quantic number which characterizes the stationary state of the nucleus, which depends on the spin numbers I of the nucleus. The total number of the possible own stationary states of the nucleus is then equal to : 2I+1. Thus the proton may exist from the point of view of its spin momentum in only two stationary states.
Without any magnetic field the
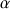and
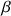have the same energy they are, so called, degenerated. It is only in a static homogenous magnetic field of value B0 and following the interaction between B0 and
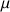that this degeneracy is suppressed (Fig.1). The separation of energy then produced is proportional to the intensity of the field B0, and creates the necessary condition for the existence of spectroscopic transition and constitutes the basis of the spectroscopy by Nuclear Magnetic Resonance.
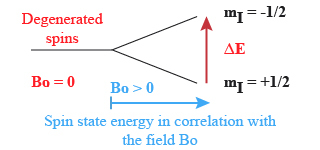
The proton will occupy the
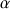state (i.e. the weakest energy one) with a higher probability.
The more the field B0 increases the more the difference of energy (or
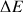) between the two spin states increases. We describe the difference of occupancy between the basic state and the excitated one with the Boltzmann law :
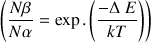
Where
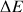is the difference of energy between the two states, k the Boltzmann constant, T the absolute temperature in °K,
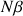the number of spins at the high energy level and
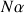the number of spins at the low energy level.
At the equilibrium only a small excess of nuclei are at the fundamental state. For a field of 1.4 T at room temperature,
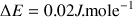. According to the theory the population excess determines the probability of excitation.
However, this population excess does not reach more than 0.001%
